
주변분포(Marginal distribution)는 이전 포스트에서 설명한 결합확률분포(Joint probability distribution) 혹은 결합밀도함수(Joint density function)와 밀접한 관계를 가지고 있는 분포이다. 결합확률분포 혹은 결합밀도함수를 전제로 성립할 수 있는 확률분포가 바로 주변분포이기 때문이다.
결합확률분포 f(x, y)에서 확률변수 X에 대한 주변분포 g(x)는 아래와 같다.
$$ g(x) = \underset{y}{\Sigma} f(x, y) $$
결합확률분포 f(x, y)에서 확률변수 Y에 대한 주변분포 h(y)는 아래와 같다.
$$ h(y) = \underset{x}{\Sigma} f(x, y) $$
결합밀도함수 f(x, y)에서 확률변수 X에 대한 주변분포 g(x)는 아래와 같다.
$$ g(x) = \int_{-\infty}^{\infty} f(x, y) dy $$
결합밀도함수 f(x, y)에서 확률변수 Y에 대한 주변분포 h(y)는 아래와 같다.
$$ h(y) = \int_{-\infty}^{\infty} f(x, y) dx $$
이전 포스트에서 다룬 결합확률분포의 예제를 응용하여 주변분포를 살펴보도록 하자.

위의 예제에서 f(x, y)는 아래와 같다.
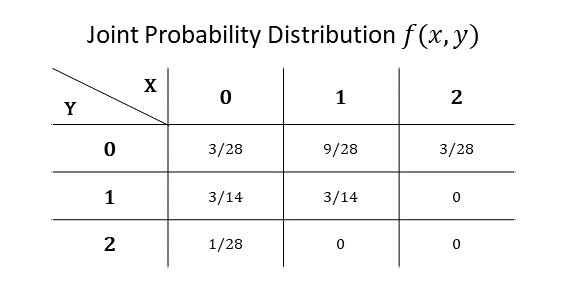
위와 같은 결합확률분포에서 주변부, 즉 아래와 같은 도표를 바로 주변분포라고 한다.

예를 들어, 위의 결합확률분포 f(x, y)를 전제로 한 주변분포 g(x)는 g(0) = 5/14, g(1) = 15/28, g(2) = 3/28으로 계산할 수 있고, h(y)는 h(0) = 15/28, h(1) = 3/7, h(2) = 1/28인 것으로 계산할 수 있다.
특이사항으로는, 주변분포의 값을 모두 더하면 다른 확률분포가 그러하듯 1의 값이 나온다는 것이다.
주변분포는 두 개의 변수를 가진 결합확률분포 및 결합밀도함수를 하나의 변수를 가진 함수로 변환하는 데에 의의가 있다.
'통계학 > 기초 통계' 카테고리의 다른 글
| [기초 통계] 20. 기댓값: Expected Value (0) | 2023.02.05 |
|---|---|
| [기초 통계] 19. 조건부 분포: Conditional Distribution (0) | 2023.02.02 |
| [기초 통계] 17. 결합밀도함수: Joint Density Function (0) | 2023.01.30 |
| [기초 통계] 16. 결합확률분포: Joint Probability Distribution (0) | 2023.01.25 |
| [기초 통계] 15. 연속확률변수의 누적분포함수: Cumulative Distribution Function of Continuous Random Variable (0) | 2023.01.25 |




